Предсказуем ли рынок? Per aspera ad astra

По мере того, как фондовый рынок играл всё большую роль не только в экономике, но и в политике, и в социальной жизни, за ним стали следить не только непосредственныe участники, но и люди, не имеющие к рынку прямого отношения. Банкротство одной из первых печально знаменитых <пирамид> - вест-индской компании во Франции - и фондовый крах конца 20-х годов прошлого века, с которого началась Великая депрессия, сделали фондовый рынок объектом внимания широких слоев населения. Поэтому прогноз ситуации на нем как средство <борьбы> с неопределенностью будущего приобретал все большее значение. Эта информация могла повлиять на принятие политических решений или вызвать волну социальных потрясений. Поэтому неудивительно, что вопрос о предсказуемости рынка обратил на себя внимание серьезных учёных. Со свойственной им основательностью и широтой был поставлен вопрос: а предсказуем ли рынок, в принципе?

Классический период

На ход рассуждений по этому поводу сильное влияние вначале оказали известное из физики броуновского движения и центральная предельная теорема. Английский физик Броун обнаружил замечательное явление: если маленькую крошку краски поместить в жидкость, то она не остаётся на месте, а начинает беспорядочно двигаться, причём интенсивность движения растает с увеличением температуры.

Объяснение было предложено следующее: жидкость состоит из невидимых глазом маленьких частиц, которые находятся в непрерывном движении. Мы не можем наблюдать его в силу размеров частиц, зато мы видим движение маленькой частички краски, обусловленное миллионами столкновений между ней и частицами жидкости. Поскольку частицы в жидкости движутся независимо друг от друга, количество их крайне велико и все они одинаковы, соударения происходят случайно, и суммарный передаваемый импульс также является случайной величиной, распределённой, в силу центральной предельной теоремы, по нормальному закону. Это объяснение не позволяет предсказать точное движение конкретной частицы, зато даёт возможность получить статистические оценки ее траектории, найдя математическое ожидание и дисперсию смещения относительно начального положения.

Поскольку приведенные рассуждения оказались эффективными для молекулярной физики, была предпринята попытка использовать их для объяснения динамики фондового рынка. Пробной частицей здесь является конкретный актив или рыночный индекс, координатой одномерного движения - его цена, частицами жидкости - участники рынка. Как следствие - цена представляет собой случайное блуждание, каковым является броуновское движение.

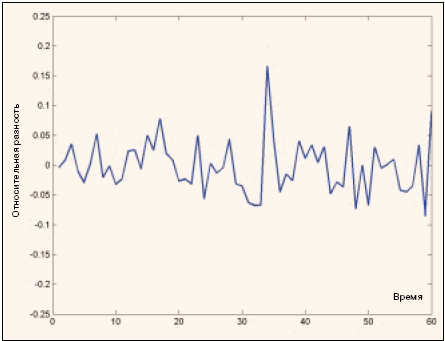
Рис. 1-а. Реальный исторический ряд.

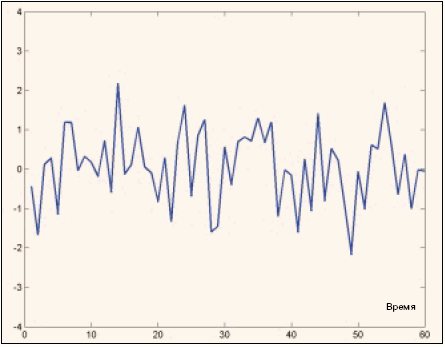
Рис. 1-б. Искусственный временной ряд.

Внешняя похожесть реальных исторических данных и искусственных временных рядов, смоделированных в рамках сделанных предположений (рис. 1-а и 1-б), предопределила уверенность исследователей в таком объяснении динамики цен и породила гипотезу эффективного рынка. Если перевести требования, при которых применим аппарат броуновского движения, с математического языка на бытовой, получится следующее:

- участники рынка должны действовать независимо друг от друга;

- количество участников торгов на каждом активе должно быть крайне велико;

- актив должен свободно покупаться и продаваться в любом количестве (иметь бесконечную ликвидность);

- все участники должны иметь одинаковый инвестиционный горизонт;

- все они должны располагать одинаковой информацией об активе;

- все должны незамедлительно реагировать на эту информацию;

- реакция на новую информацию должна быть рациональной (при отрицательной информации нужно продавать, при положительной - покупать).

Приведенные выше предположения получили название - гипотеза эффективного рынка (ГЭР), которая была теоретическим фундаментом для множества построений, имеющих, в том числе, и практическую направленность. В первые годы после появления ГЭР многим казалось, что решение вопроса о прогнозируемости рынка получено. В общем, можно было бы ставить точку, но...

Первыми забили тревогу практикующие трейдеры и финансовые менеджеры. Оказалось, что резкие скачки в ценах активов происходят гораздо чаще, чем это следовало из нормального распределения. Так как на сильных колебаниях и происходят наибольшие потери, это предопределило интерес к <толстым хвостам>. Но найти решение проблемы в рамках ГЭР не удалось.

Кроме того, появились и другие вопросы, касающиеся обоснованности предположений, заложенных в гипотезе. Например, предположение об идентичности доступной информации. В этом случае все участники рынка ведут себя рационально - предположим, продают акции. Откуда тогда, в рамках гипотезы о рациональности поведения, берется ликвидность на рынке?

Гипотеза о независимости поведения участников рынка друг от друга также порождает вопросы. Практикам, например, до боли знакома ситуация, когда трейдеры напряженно ожидают определённого движения рынка (например, падения). В этот момент достаточно небольшой флуктуации цены вниз, чтобы на рынок обрушилась лавина заявок на продажу.

В таких случаях типичное объяснение действий участников рынка звучит так: <Я ожидал, что цена пойдёт вниз, а тут как стали все продавать... Вот и я, чтоб успеть...>. Налицо явный синергизм (взаимовлияние) в действиях трейдеров.

Еще один очевидный вопрос касается одинакового временного масштаба торгов участников рынка. В силу того, что временной горизонт игроков различается, то и значимой для них окажется разная информация.

И, наконец, действительно ли одинаковая информация доступна частному инвестору и профессиональному менеджеру, непосредственно находящемуся на торговой площадке? Несколько последних Нобелевских премий, выданных за модели рынка с асимметричной информацией, свидетельствуют об обратном, как, впрочем, и последние корпоративные скандалы в США.

Новые ветра

Одним из событий, заставивших исследователей пойти на основательную ревизию гипотезы случайного блуждания цен, стало появление нового физического понятия - детерминированного хаоса. Оказалось, что шумоподобные временные ряды могут быть порождены системой, в которой нет ни одного случайного элемента. На рис. 2-а приведён пример центрированного логистического отображения, являющегося самым простым примером детерминированного хаоса и выражающегося уравнением

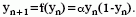
Рис. 2-а. Пример центрированного логистического отображения

Очевидно визуальное сходство модельного ряда с реальным графиком цены какого-нибудь актива. На рис. 2-б можно увидеть прогноз этой последовательности, выполненный нейронной сетью. Прогноз выполнялся на одну точку вперёд.

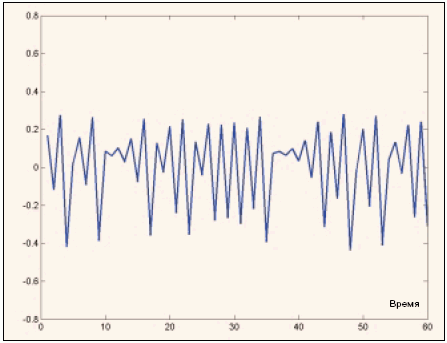
Рис. 2-б. Реальные и прогностические изменения цен.

Общее количество таких одношаговых прогнозов равно 50. Очевидно, что, если бы с такой точностью прогнозировались реальные приращения цен, этого было бы более чем достаточно для практического извлечения прибыли. Однако формальное применение такой же нейросети для прогноза ряда реальных приращений цены даёт другой - неудовлетворительный результат.

Итак, первая проблема, с которой пришлось столкнуться на пути применения теории детерминированного хаоса к финансовым рядам, заключается в следующем: почему внешне похожие шумоподобные ряды по-разному поддаются прогнозу? Существует ли какое-нибудь характерное свойство, отличающее эти ряды? Вскоре были найдены ответы и на эти вопросы.

Рассмотрим фазовый портрет логистического отображения (рис. 3-а). Оказывается, что в фазовом пространстве, заданном задержанными во времени значениями последовательности, существует некоторое множество, за пределы которого <случайные> значения ряда не выходят. В данном случае это кривая, представляющая собой параболу. С увеличением длины последовательности растет только степень заполнения этой кривой. Ее положение и форма не меняются.

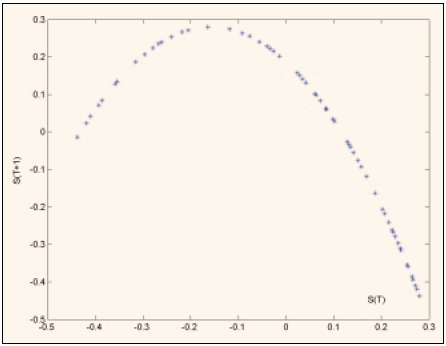
Рис. 3-а. Фазовый график логистического отображения.

Такие множества в фазовом пространстве, к которым притягиваются (или вовсе от них не отклоняются) фазовые траектории, и которые изображают динамический процесс, называются аттракторами. Поскольку в задержанных на один шаг координатах аттрактор представляет собой параболу, есть смысл искать будущее значение хаотической последовательности как квадратичную функцию от предыдущего значения. Коэффициенты квадратичной зависимости подбираются по исторической реализации методом наименьших квадратов. После этого можно построить прогноз. На самом деле существует ряд проблем, связанных с точностью определения внутренних параметров. Дальнейшее поведение ряда крайне чувствительно как к начальным условиям, так и значению этих управляющих параметров. Поэтому достаточно точный прогноз на любое количество шагов невозможен. Оценка количества шагов, на которое может быть предсказан хаотический ряд, представляет собой тему отдельного исследования. Сейчас же можно сказать, что после произведенных усилий возможен прогноз на несколько шагов вперёд. Каков же аттрактор у ряда реальных приращений цены? Ответ на этот вопрос даёт рисунок 3-б.

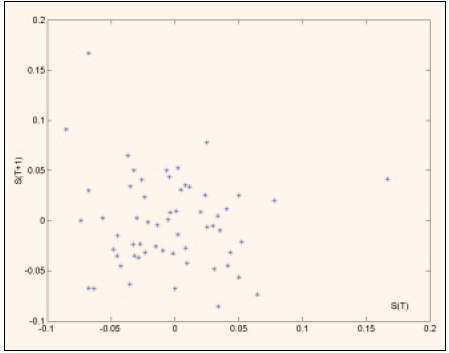
Рис. 3-б. Фазовый график реального процесса.

Как видно, ярко выраженного аттрактора, наподобие параболы в логистическом отображении, нет. Поэтому и прогноз реальных приращений цены, выполненный по той же схеме, что и для логистического уравнения, не принёс ожидаемых результатов. Итак, наличие или отсутствие аттрактора объясняет хорошую или плохую прогнозируемость ряда. У детерминированного хаоса аттрактор есть, у реальных цен его нет - этот очевидный вывод лежит нa поверхности. Возникает классический русский вопрос: что же делать?

Что делать?

Как гласит народная мудрость, у любой, сколь угодно сложной проблемы всегда существует очевидное, простое для понимания, неправильное решение. Это относится и к нашему случаю. Вывод об отсутствии аттрактора у ряда реальных приращений цены был преждевременным. Аттрактора нет в тех же координатах, что и для логистической последовательности. Но это вовсе не означает, что его нет вообще! Во-первых, аттрактор может существовать в тех же координатах, но с другим временем задержки. Во-вторых, почему он должен быть одномерным, как у логистического уравнения? Будущее может зависеть не от одного предыдущего значения, а от нескольких.

Если принять точку зрения А. Пуанкаре, положившего начало исследованию таких отображений, то можно представить рынок как сложный динамический процесс взаимодействия различных факторов, большинство из которых нам недоступно для наблюдения. А его видимой проекцией является рыночный индекс. Итак, можно ли, наблюдая лишь за одной проекцией многомерного аттрактора, оценить его настоящую размерность (количество информации, необходимое для построения прогноза)?

До недавнего времени вопрос казался неразрешимым. Но в 1981 году математик Тэйкенc доказал теорему, согласно которой некоторые общие свойства целого аттрактора сохраняются и в его проекции. Таким общим свойством является вложенная размерность аттрактора, или, как назвал её Тэйкенс, размерность предельной ёмкости. Оценка вложенной размерности даёт ответ на вопрос об истинной размерности аттрактора. А сколько задержанных координат наблюдаемой проекции нужно брать, чтобы адекватно спроецировать реальный аттрактор на пространство, задаваемое этими координатами? По замечанию Рюэля, их нужно брать не менее чем удвоенная величина вложенной размерности.

Остался еще вопрос по поводу выбора <правильного> времени задержки при формировании пространства в задержанных координатах. Согласно теоремам Тэйкенса и Манэ, для бесконечного ряда при отсутствии шума время задержки можно выбрать почти произвольно. Однако на практике (наблюдаемая выборка конечна и в ней априори присутствует шум) выбор существенно влияет на качество получаемой проекции и, как следствие, на то количество информации, которое из неё можно извлечь. Для описания d-мерного пространства, на котором восстанавливается фазовый портрет, предлагается брать d максимально независимых координат наблюдаемого ряда. Это позволяет <рассматривать> проекцию аттрактора под оптимальным <углом зрения>.

Что дальше?

Закрывают ли полученные ответы все вопросы в области предсказуемости рынка? Нет, не закрывают. Остаются ещё несколько вопросов, ответов на которые пока нет. Например, неизвестно, в каком классе функций искать зависимость будущего от прошлого. В случае одномерного хаоса у нас была возможность увидеть, что зависимость аппроксимируется параболой. Такой возможности не будет уже при размерностях аттрактора выше трёх. Еще один вопрос. Как показывают наши исследования, для рынка не характерны стационарные законы и взаимосвязи. В отличие от математических законов, рыночные закономерности носят краткосрочный характер, и со временем структура рынка меняется. Рыночные показатели, связанные в один момент времени, не связаны в другой, и наоборот.

В терминах фазовых портретов это означает, что все найденные параметры меняются со временем: размерность фазового пространства, время задержки, внутренние параметры уравнений и даже сам класс функциональных зависимостей. Наглядно дыхание рынка показывает рисунок 4.

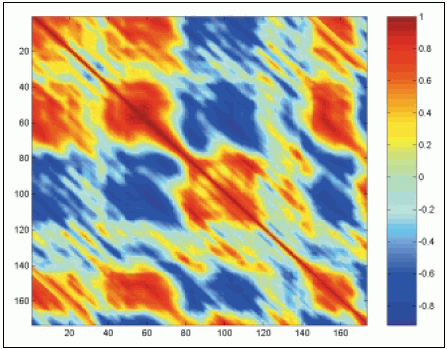
Рис. 4. Изменение соотношения между ценами открытия и закрытия с течением времени (пояснения в тексте).

На рисунке изображено <взаимодействие> между двумя значениями цены - Open и Close - с течением времени. По горизонтальной оси отложено время задержки одного ряда относительно второго. По вертикальной оси - наоборот, время задержки второго ряда относительно первого. Физическое время направлено из верхнего левого угла в правый нижний. Эта диагональ соответствует нулевому смещению рядов друг относительно друга и отражает мгновенное взаимодействие этих показателей (без запаздывания и опережения).

Цветом обозначены сила и направление взаимной динамики показателей: тёмно-красный цвет означает корреляцию рядов, тёмно-синий - антикорреляцию. Если теперь проследить любую диагональ, идущую из левого верхнего угла в нижний правый, можно увидеть, как менялось взаимовлияние показателей с течением времени. В одно время ряды антикоррелировали, затем наступали времена, когда они вообще никак не влияли друг на друга, потом наступал период противофазной динамики. Такова природа рынка. И надеяться описать её одной моделью, построенной раз и навсегда, было бы наивно. Это выдвигает требования к адаптивности моделей и методов, применяемых для прогноза и анализа рынка.

Увы, существуют и другие нерешённые вопросы. Тем не менее первые шаги к решению проблемы предсказуемости рынка (в частности, фондового) сделаны. Таким образом, ответить на вопрос, вынесенный в заглавие данной статьи, можно утвердительно, оговариваясь только, что не все активы предсказываются одинаково хорошо. Более того, периоды <предсказуемости> могут сменяться периодами <непредсказуемости>. Поскольку существуют математические <инструменты>, отвечающие на данные вопросы, специалисты могут использовать их во вполне практической плоскости - прогнозировать как поведение рынка в целом, так и <метание> конкретных акций со степенью точности, достаточной для извлечения прибыли.

2002

Владимир Черкашенко, Сергей Вечерин